
I agree about having to have a good understanding of what is happening, everything makes much more sense when it is understood what's going on. In other words, there should be numbers r and s giving #\vec#. The point is that if the three vectors are coplanar, then (unless they all point along a single line), one of them will be a linear combination of the other two. However, it would be better if you really understood what is happening, rather than just plugging in formulas you do not fully grasp. At least this is what I have gathered from a little bit of research.Īppreciate it if someone could double check the thinking behind the method. But as I am extremely new to this (the past half hour or so) I wanted a second opinion.Īnd therefore as the determent is zero, that means they are NOT linearly independent, and hence means that they are coplanar.
So where I found this out, it had a few example of testing for linearly independency using the determent of a matrix formed by the three vectors (as column vectors) and I think I have done it correct as my answer comes out to zero. Any external agent that is responsible for producing a change in the condition of rest or motion is called a force.

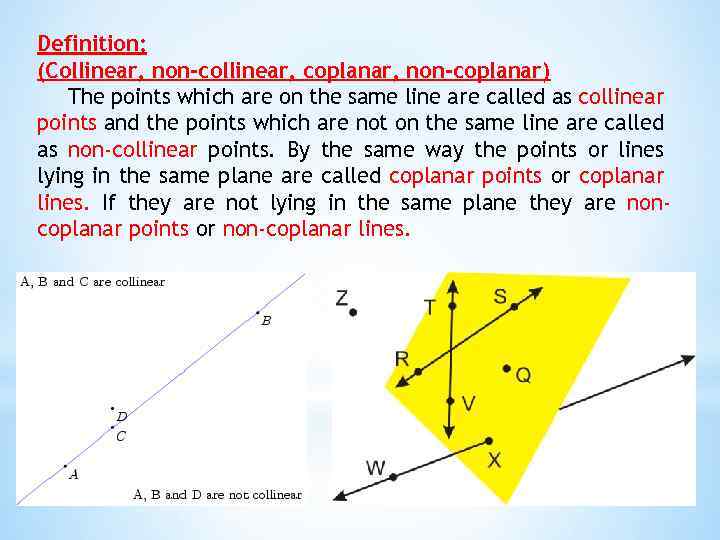
So I did a little research and found that one way is to test if they are linearly independent and that if that are not linearly independent then that means they must be coplanar. Coplanar Force System is a system of forces acting on the same plane. If two non-vertical lines in the same plane intersect at a right angle then they are said to be perpendicular. Prove that the vectors a=(3,2,-1), b=(5,-7,3), c=(11, -3, 1) are coplanar.įirst time I have ever came across the term coplanar, I know what it means but did not know any tests for it. Points, lines, or shapes are non-coplanar if they do not lie in the same plane.


 0 kommentar(er)
0 kommentar(er)
